みなさんこんにちは！

低学年クラスで「二十面体」を作りました。
今回は、展開図を描いて組み立てるのではなく、少し変わった方法で作って行きます。

名刺から二十面体を作る

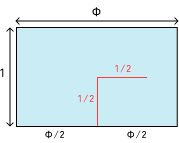
名刺を３枚用意し、図の赤線のように切れ込みを入れます。
切れ込みをいれた名刺３枚は、写真の形に組み合わせることができます。

組み合わせた名刺の角を結ぶと、不思議なことに「二十面体」が出来上がるのです！

なぜ二十面体ができるのか？

正二十面体は、頂点を中心に５つの正三角形が並んでいます。
ある視点からみると、「正五角形」になっていることがわかります。

正五角形には、１辺と対角線が「黄金比」であるという性質があり、
名刺にも、短辺と長辺が「黄金比」である性質があります。

この「黄金比」という共通点があることで、
直行した３枚の名刺の角が正二十面体の頂点座標と重なり、
正二十面体が現れる、というわけなのです。

（ただ、日本の一般的な名刺サイズは黄金比ではありません…。
そのため、正二十面体ではなく、正確には「二十面体」になる点、ご注意ください。）

子どもたちと作ってみた

名刺の組み合わせに少し苦戦していましたが、
糸をかけて線を結ぶ作業は器用に進めてくれました！

まとめ

正二十面体に隠れた「黄金比」を、見つけることができたかな？
一つの立体にも色々な性質があって面白いものです。

作ったり観察しながら、立体の面白さ・算数の不思議を感じてもらえたら嬉しいです。

一緒に学ぶ塾生を募集しています

算楽塾では、算数を楽しみ・苦手意識をなくすことを大切にさまざまな授業を行なっています。

「算数に苦手意識がある」「もっと楽しく算数を学びたい」「知識より考える力を育てたい」

そんな方のお力になれるかもしれません。
算数教育に関するご相談、無料体験受付していますので、どうぞお気軽にご連絡ください😊